Introduction

Generally, separate content from style in natural images is still an extremely difficult problem. However, the recent advance of DCNNs has produced powerful computer vision systems that learn to extract high-level semantic information from natural images. Therefore, we can extract the style and content from one image to another. Transferring the style from one image to another is a problem of texture transfer. In texture transfer, the goal is to synthetize a texture from a source image while constraining the texture synthesis in order to preserve the semantic content of a target image. For texture synthesis, there exist a large range of powerful non-parametric algorithms that can synthetize photorealistic natural textures by resampling the pixels of a given source texture. Therefore, a fundamental prerequisite is to find image representations that independently model variations in the semantic image content and the style in which is presented.

As we can see, the generated image is having the content of the Content image and style image. This above result cannot be obtained by overlapping the image. So the main question are: What is neural style transfer? how we make sure that the generated image has the content and style of the image? how we capture the content and style of respective images?

What is neural style transfer?

Neural Style Transfer(NST) is the technique which generated an image G containing a style of image A and the content of image C. It deals with two sets of images: Content image and Style image. This technique helps to recreate the content image in the style of the reference image. It uses Neural Networks to apply the artistic style from one image to another. NST opens up endless possibilities in design, content generation, and the development of creative tools.

How does NST work?

The goal of NST is to give to the deep learning model the ability to differentiate between style and content representations. NST uses a pre-trained convolutional neural network with additional loss functions to transfer the style and then, generate a new image with the desired features. Style transfer works by activating the neurons in a specific way, so that the output image and the content image match particularly at the content level, while the style image and the desired output image should match in terms of texture and capture the same style characteristics in the activation maps. These two objectives are combined in a single loss formula, where we can control how much we care about style reconstruction and content reconstruction.

The loss function in neural style transfer plays a crucial role in guiding the model to generate an image that combines both the desired style and content. We have two functions loss : content loss and style loss. The loss function is used to quantify how well the generated image matches the style and content objectives. It measures the difference between the network activations for the original content image and the generated image, as well as the difference between the network activations for the original style image and the generated image.

To balance style reconstruction and content reconstruction, the loss function combines these two differences using weights. These weights control the relative importance of style reconstruction compared to content reconstruction. Optimizing the loss function involves adjusting the pixel values in the generated image to minimize the difference between the network activations for the original content image and the generated image, while also minimizing the difference between the network activations for the original style image and the generated image.

By adjusting these pixel values, the model learns to reproduce the desired style characteristics in the corresponding areas of the generated image while preserving the content information from the original image. Thus, the loss function optimizes the model to generate an image that combines the desired style and content by minimizing the discrepancies between the network activations for the reference images and the generated image.

Here are the required inputs to the model for image style transfer:

1. A Content Image –an image to which we want to transfer style to
2. A Style Image – the style we want to transfer to the content image
3. An Input Image (random) – this will contain the final blend of content and style image

NST basic structure

Training a style transfer model requires two networks: a pre-trained feature extractor and a transfer network.

In the case of Neural Style Transfer, we use a model pre-trained on ImageNet, such as VGG using TensorFlow. Since the VGG model cannot understand images directly, it is necessary to convert them into raw pixels, afterwards feed that pixels to the model to transform them into a set of features, which is usually done by CNNs. We will see in the next section.

Thus, the VGG model acts as a complex feature extractor between the input layer (where the image is fed), and the output layer (which produces the final result). To achieve style transfer, we focus on the middle layers of the model that capture essential information about the content and style of the input images. During the style transfer process, the input image is transformed into representations that emphasize image content rather than specific pixel values.

Features extracted from upper layers of the model are more closely related to the image content. To obtain a representation of the style from a reference image, we analyze the correlation between the different filter responses in the model.

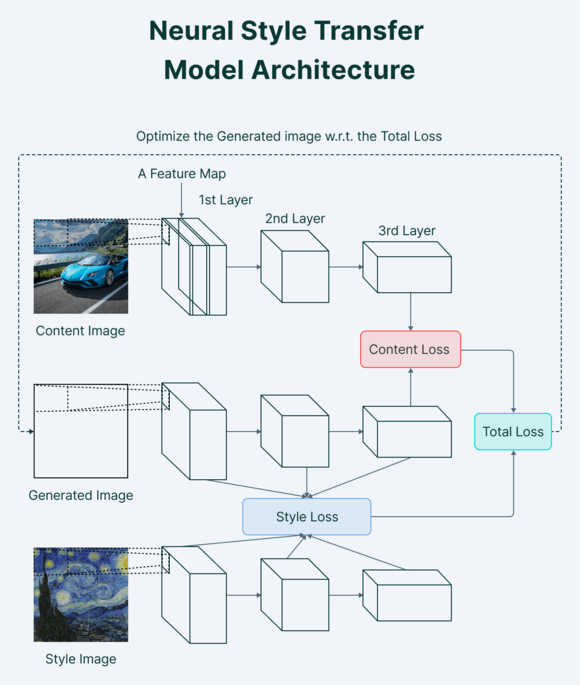Neural Style Transfer architecture diagram according to V7Labs

How CNN capture features in VGG model?

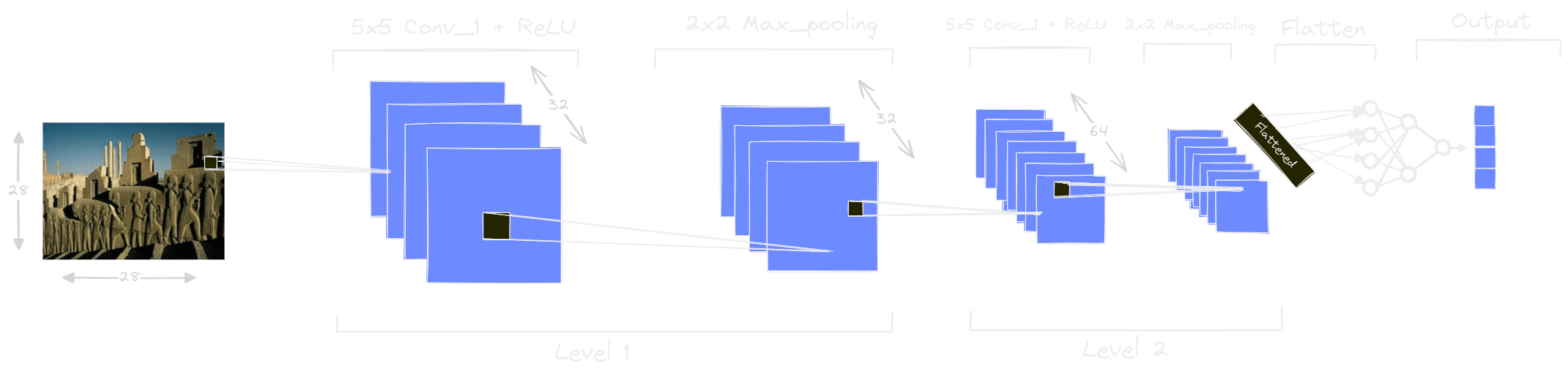
The VGG model is actually a type of CNN. VGG, which stands for Visual Geometry Group, is a very popular CNN architecture widely used in computer vision tasks, especially in the field of image classification. The VGG model is composed of several stacked convolutional layers, followed by fully connected layers. These convolutional layers are responsible for extracting visual features from images. Specifically, VGG’s convolutional layers are designed to analyze visual patterns at different spatial scales. Each convolutional layer uses filters that are applied to images to detect specific patterns, such as edges, textures or shapes.

The figure shows an exemple of CNN layers of VGG model. The first convolutional layers of VGG (those at level 1 with 32 filters) capture low-level features, such as simple edges and textures, while the deeper convolutional layers (those at level 2 with 64 filters) capture features of higher level like complex shapes and overall structures.

Thus the VGG model as a CNN is able to extract meaningful visual features from images. These features can then be used in different tasks, such as image classification or style transfer. In the context of style transfer, the model is used primarily as a feature extractor. VGG’s convolutional layers are leveraged to capture content and style information from input images, allowing these two aspects to be separated and combined to generate a new image that combines the content of a reference image and style from another image.

Content loss

Content loss is a metric that helps to establish similarities between the content image and the image generated by the style transfer model. The idea behind it is that the higher layers of the model focus more on the features present in the image, i.e. the overall content of the image. The calcul of content loss is more easy because by only working with grayscale images when calculating content loss, one focuses only on the structure and arrangement of shapes/objects in the image, without considering color or other stylistic elements. The content loss is calculated using the MSE between the upper-level intermediate feature representations of the generated image (x) and the content image (p) at layer $l$.

$L_{content}(\vec{p},\vec{x},l) = \frac{1}{2}\sum_{i,j}(F_{ij}^{l}(x) - P_{ij}^{l}(p))^2$

In this equation, $F_{ij}^{l}(x)$ represents the feature representation of the generated image x at layer $l$ and $P_{ij}^{l}(p)$ represents the representation of characteristics of the content image p at layer $l$.

Style loss

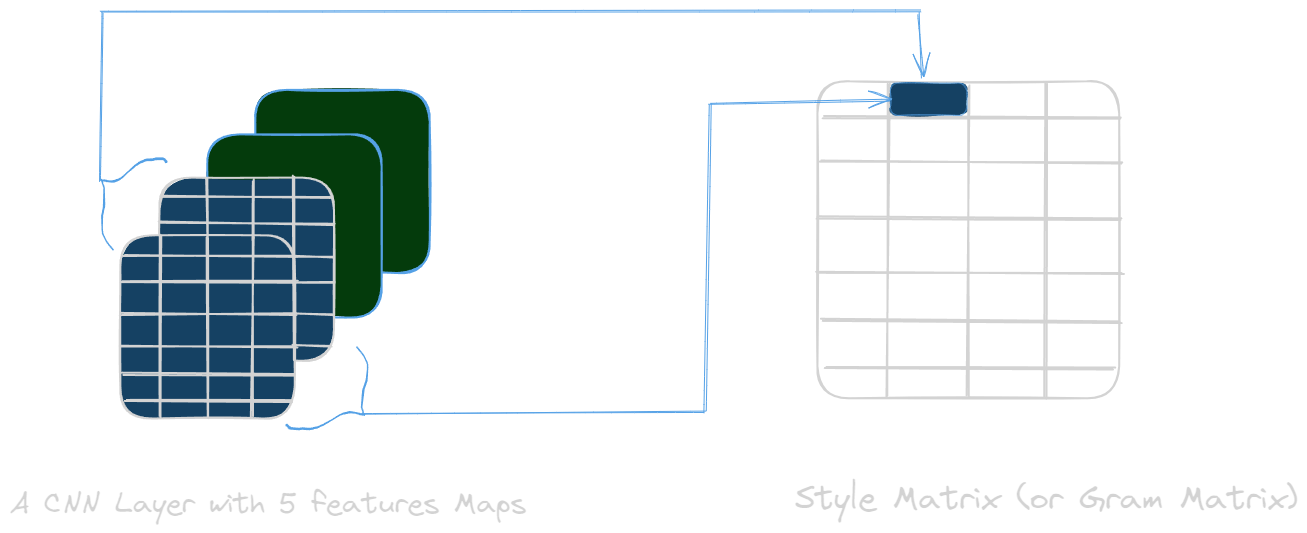
Style loss is a bit more complicated that content loss because style is hard to define exactly. It is not possible to simply compare the features like patterns, contours, shapes of the two images to obtain the style loss. We need to find the correlation between features. That is why we use another tool called: Gram matrix. The Gram matrix then captures the correlations between style characteristics. It measures how visual patterns co-occur in the image (colors, textures). More precisely, each case of the Gram matrix corresponds to the scalar product between two column vectors of the feature matrix. This allows you to obtain a signature of the image style in the form of a matrix.The Gram matrix has 2 specificities:

• The Gram matrix does not take into account the position of the features

The content loss calculation takes into account the position of each pixel in order to reproduce the content of the original image in the generated image. Conversely, the loss of style is more about textures, colors and other overall aspects independent of position. This is why the Gram matrix is ​​used to capture the stylistic features present in the image.

The first layers of a neural network encode features such as colors and textures. One might think that focusing on these layers as with the loss of content would result in a “loss of style”. However, activation maps encode both the characteristics present but also their precise location.

This is where the Gram matrix comes in useful. By eliminating the spatial component, it focuses only on feature types without considering their position. Since the objective of style transfer is to reproduce global patterns and textures rather than local details, this representation without spatial location is better suited. It highlights correlations between features regardless of their position in the image.

• The Gram matrix take the correlations of two features

When a neural network analyzes an image, each neuron in a layer will be specialized in detecting a particular visual pattern such as lines, circles or squares. The strength of activation of a neuron will then indicate the presence of this pattern. However, style depends not only on the presence or absence of individual patterns, but also on how they interact with each other.

This is where the Gram matrix comes into play in a relevant way. Indeed, we have seen that it does not take into account the position of features, placing much more emphasis on textures, colors and other overall aspects of the style. Additionally, it makes it possible to quantify the correlation between the activations of different neurons, revealing the extent to which two patterns tend to appear together consistently across the entire image.

This information on the relationships between visual patterns then makes it possible to define the style globally and independently of the precise position of each element. During style transfer, the objective is precisely to match these global patterns between the source and target image, rather than local details. By offering a representation focused on the relationships between characteristics, the Gram matrix thus facilitates comparison and guidance of the transfer process.

These two caracteristics of Gram matrix enables to retrieve style of an image by calculate style loss. So the style loss is calculated by the distance between the gram matrices (or, in other terms, style representation) of the generated image and the style reference image.

The contribution of each layer in the style information is calculated by the formula below: $E_l=\frac{1}{4 N_l^2 M_l^2} \sum_{i, j}\left(G_{i j}^l-A_{i j}^l\right)^2$ where $G_{i j}^l$ is the Gram matrix of style image and $A_{i j}^l$ is Gram matrix of generated image

Thus, the total style loss across each layer is expressed as: $L_{\text {style }}(a, x)=\sum_{l \in L} w_l E_l$

Total Loss

The total loss function is the sum of the cost of the content and the style image. Mathematically,it can be expressed as :

$L_{total}(\vec{p}, \vec{\alpha},\vec{x}) = \alpha L_{content}(\vec{p}, \vec{x}) + \beta L_{style}(\vec{\alpha}, \vec{x})$

You may have noticed Alpha and Beta above. They are used for weighting Content and Style cost respectively. In general, they define the weightage of each cost in the Generated output image.

Once the loss is calculated, then this loss can be minimized using backpropagation which in turn will optimize our randomly generated image into a meaningful piece of art.

Conclusion

In this article, we were able to discover a fascinating application of deep learning with neural style transfer. By separating the content and style of different works, models like Neural Style are able to combine their respective styles in stunning ways. Although still imperfect, the results obtained using pre-trained networks like VGG demonstrate the potential of this approach to generate new, never-before-seen artistic creations. Beyond the fun aspect, style transfer also opens up perspectives for image editing and retouching. We have seen that current work attempts to refine the separation of content and style, or to extend these techniques to other media such as video. In the future, more advanced models could further assist human creativity. But beyond the applications, style transfer above all illustrates the astonishing capacity that artificial intelligence has to understand and imitate complex visual styles, thanks to recent advances in deep learning.